Coorbit theory
In mathematics, coorbit theory was developed by Hans Georg Feichtinger and Karlheinz Gröchenig around 1990.[1][2][3] It provides theory for atomic decomposition of a range of Banach spaces of distributions. Among others the well established wavelet transform and the short-time Fourier transform are covered by the theory.
The starting point is a square integrable reprentation  of a locally compact group
of a locally compact group 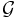 on a Hilbert space
on a Hilbert space 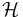 , with which one can define a transform of a function
, with which one can define a transform of a function 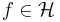 with respect to
with respect to 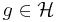 by
by 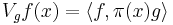 . As mentioned above it is important to note that many important transforms are special cases of the transform, e.g. the short-time Fourier transform and the wavelet transform for the Heisenberg group and the affine group respectively. Representation theory yields the reproducing formula
. As mentioned above it is important to note that many important transforms are special cases of the transform, e.g. the short-time Fourier transform and the wavelet transform for the Heisenberg group and the affine group respectively. Representation theory yields the reproducing formula 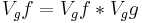 . By discretization of this continuous convolution integral it can be shown that by sufficiently dense sampling in phase space the corresponding functions will span a frame for the Hilbert space.
. By discretization of this continuous convolution integral it can be shown that by sufficiently dense sampling in phase space the corresponding functions will span a frame for the Hilbert space.
An important aspect of the theory is the derivation of atomic decompositions for Banach spaces. One of the key steps is to define the voice transform for distributions in a natural way. For a given Banach space  , the corresponding coorbit space is defined as the set of all distributions such that
, the corresponding coorbit space is defined as the set of all distributions such that 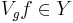 . The reproducing formula is true also in this case and therefore it is possible to obtain atomic decompositions for coorbit spaces.
. The reproducing formula is true also in this case and therefore it is possible to obtain atomic decompositions for coorbit spaces.
References
- ^ H. G. Feichtinger and K. Gröchenig. "A unified approach to atomic decompositions via integrable group representations" Lect. Notes in Math. 1302:52—73, 1988.
- ^ H. G. Feichtinger and K. Gröchenig. "Banach spaces related to integrable group representations and their atomic decompositions, I" J. Funct. Anal. 86(2):307–340, 1989.
- ^ H. G. Feichtinger and K. Gröchenig. "Banach spaces related to integrable group representations and their atomic decompositions, II" Monatsh. Math. 108(2-3):129–148, 1989.